2017年8月号の巻
挑戦状
拙者は忍者エピス丸。キミはこの問題を解けるかな?
1辺が8cmの正三角形の各頂点を中心に、半径が1辺の長さである円を3つかきます。その3つの円で囲まれた図形をアとします。この図形アの外側を半径4cmの円イがすべることなく1周するとき、円が通過する右図の斜線部分の面積を求めなさい。
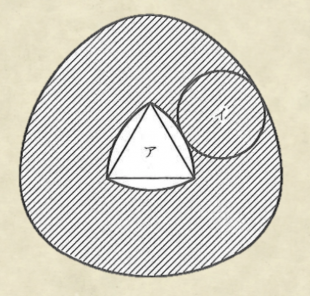
(2010年度 駒場中学東邦入試問題)
オヌシなら、まず何をする? 健闘を祈る!
攻略キーポイント
近では部屋のスミまでキレイにしてくれるロボット掃除機や、一部の自動車に使われているロータリーエンジンにも利用されておる。また、ルーローの三角形と同じ作図方法で、図形が正七角形であれば、「ルーローの七角形」が作図でき、これはイギリスの50ペンス硬貨などに利用されているぞ。

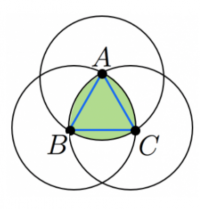
19世紀のドイツで国際的な機械工学者として活躍し、「運動学の父」と称されたフランツ・ルーロー。彼の功績として最も有名なのが、「ルーローの三角形」じゃ。正三角形の各頂点を中心に、半径がその正三角形の1辺となる弧を結んで作図することができる図形なのだ。
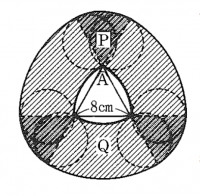
今回の挑戦状は、ルーローの三角形の周りを円が1周したときの通過部分の面積を求める問題でござる。与えられた図形だけでは問題を解くことはできないので、小学生の知識で面積を求めることができるように、図形を分割してみよう。図にあるように、6つの部分に分割するとそれぞれの面積を求めることができるぞ。さらに、6つの部分を計算するだけではなく、うまく6つの部分を切り貼りしてつなぎ合わせると、あっという間に答えが求められるぞ。実際に図形を紙に書いて切りはりしても面白いかもしれないぞ。さあ、やってみよう。

