2017年7月号の巻
挑戦状
拙者は忍者エピス丸。キミはこの問題を解けるかな?
次の筆算が成り立つような4ケタの整数ABCDを考えます。4ケタの整数ABCDが最も小さくなるのは、A= ,B= ,C= ,D= のときです。ただし、A,B,C,Dは異なる1ケタの整数を表しているものとし、■は、筆算の中の1ケタの整数を塗りつぶしたものです。
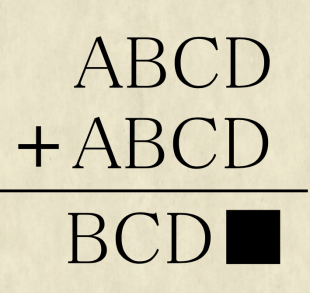
(2017年度 慶應義塾中等部 入試問題)
オヌシなら、まず何をする? 健闘を祈る!
攻略キーポイント
現代では、老若男女を問わずに楽しめる様々なパズルが存在する。ジグソーパズルや知恵の輪、コンピューターで遊べるパズルゲームなど、無数に存在するパズルたちは、我々の知的好奇心をくすぐってくれる。そんなパズルの中で、計算式の中で伏せられた数を推理する「虫食い算」。小学生向けの中学受験算数の問題として取り上げられることの多い虫食い算の歴史は、江戸時代までさかのぼる。最も古い問題は、世紀の有名な和算書「竿頭算法(かんとうさんぽう)」にあるというのだから、いかに日本人が昔からパズル好きだったかがわかるというものじゃ。今回の挑戦状は、虫食い算の中でも「覆面算」という、数が別の記号や文字に置き換えられている問題にチャレンジしてみよう。
まず攻略キーポイントのつ目は、条件を確実に把握しておくこと。筆算が成り立つような4ケタの整数が「最も小さくなる」場合を考えているということは意識しておこう。そうすると、4ケタの最も小さい数であれば、A=1で決まりじゃな。また、Bもできるだけ小さい方が良いということ、A,B,C,Dは異なるケタの整数を表しているということから、B=2も決まってしまうだろう。このように、まずは問題を正確に読み、与えられている条件をしっかりと理解することが大切じゃ。
そうなってくると、C・Dに当てはめられる数も限られてくるが、虫食い算ではときどき確信を持って数を決めることができなくなる瞬間がある。そんなときは失敗を恐れず数を当てはめてみよう。間違えた数を当てはめたら、「その数は間違っている」という一つの結果が得られるのだから、それだけでも十分な成果なのじゃ!間違いを恐れず、やってみる、「トライ&エラー」を繰り返す姿勢は、攻略キーポイントの2つ目と言えるじゃろう。恐れるものは何もないぞ!さあ計算、計算!

