2017年2月号の巻
挑戦状
拙者は忍者エピス丸。オヌシはこの問題を解けるかな?
直線ℓと直線mは垂直に交わっています。また図のように平行四辺形ABCDがあります。次の問いに答えなさい。
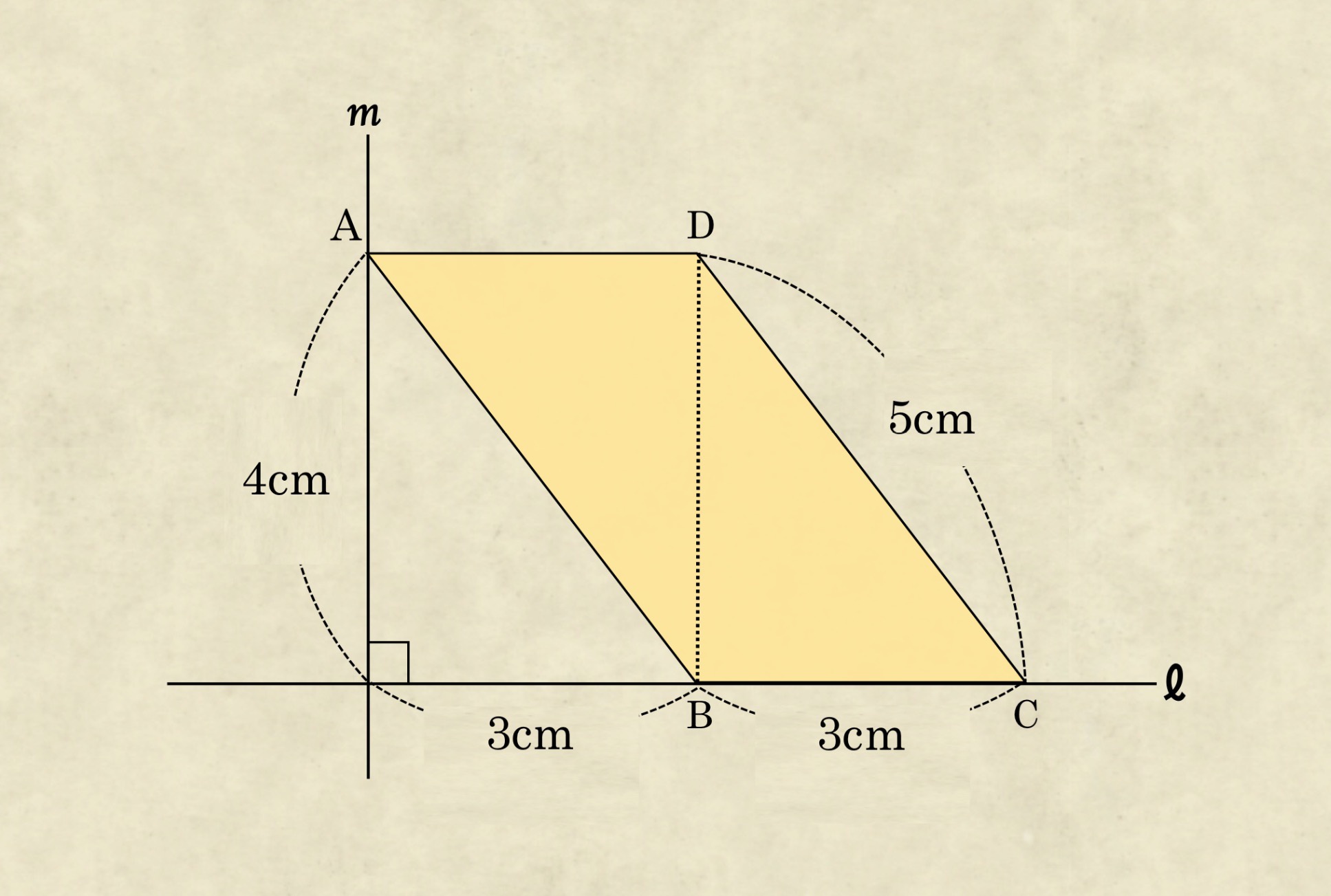
(1) 平行四辺形ABCDを直線ℓのまわりに1回転させてできる立体Pの体積を求めなさい。円周率は3.14とします。
(2) 平行四辺形ABCDを直線mのまわりに1回転させてできる立体をQとします。Pの体積とQの体積の比を求めなさい。
(2012年度 高槻中学 入試問題)
オヌシなら、まず何をする? 健闘を祈る!
攻略キーポイント
【攻略キーポイント】
今回は立体図形でござる。定規やコンパスを使わなくても、フリーハンドで線を引っぱり、書き上げた図形をまっすぐ動かしたり回転させたりすることは、とても楽しい作業じゃな。絵を描くことが好きな人は、それだけで図形センスがあると言っても良いぞ。
ではさっそく「お絵描き」してみよう。
円すいを回転させたときの通過部分がどんな立体図形なのかは、問題に書かれていない。頭の中にイメージするために見取り図を書こう。回転体の見取り図を書く手順は、「軸の左右に回転させる図形を書く」「対応する頂点をだ円で結ぶ」、この2つだけ。手順を終えると、下の図のようになるぞ。
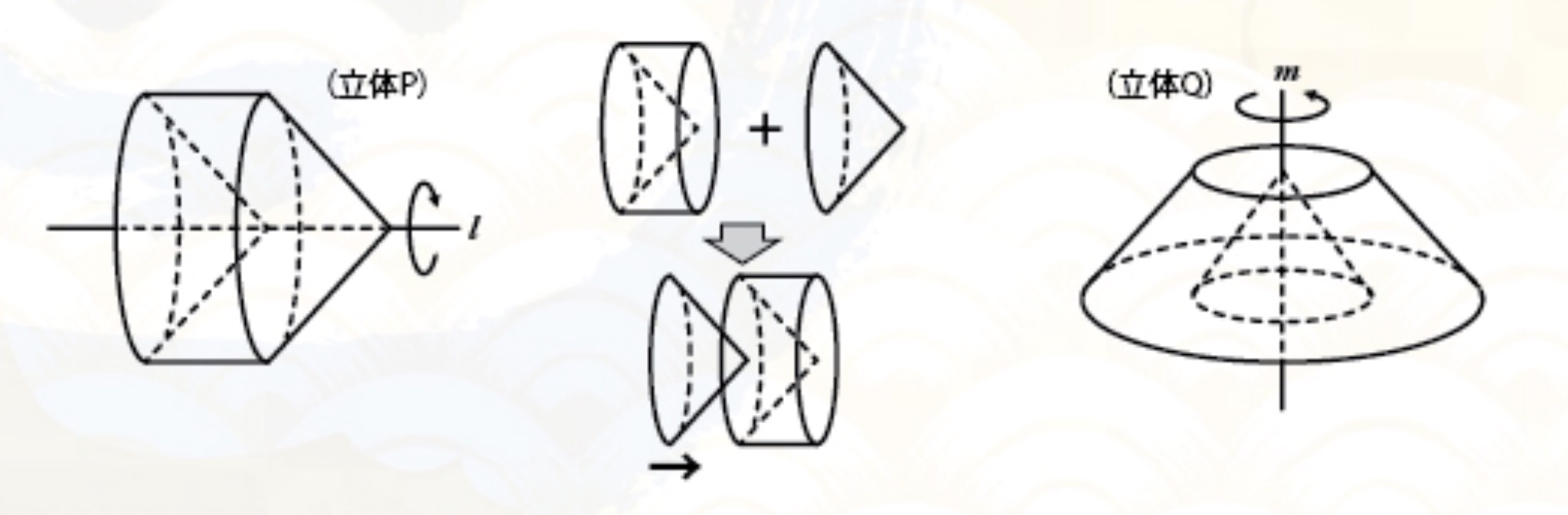
ここまで書けたら、知っている立体図形のイメージと近いものがないか考えてみよう。では(1)のヒント。よ〜く見取り図を見てみると、円柱から円すいをくり抜いた立体と、円すいが合わさった立体図形だということがわかる。円すいを円柱のくり抜いた部分にスッポリはめてみたら・・・円柱の出来上がりじゃ!(2)は体積比を利用するぞ。これは自分でやってみよう。
さあ、もうすでに見通しは立っておるな。あとは計算あるのみじゃ!

