2016年11月号の巻
挑戦状
拙者は忍者エピス丸。オヌシはこの問題を解けるかな?
半径3cmの円の周上に点Aがあります。
点Aを中心として、この円を30°回転させてできる円があります。
斜線部の面積を求めなさい。
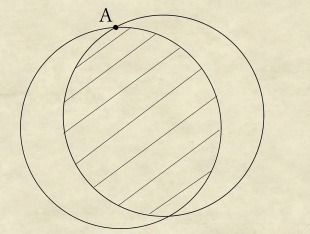
(2013年度 麻布中学 入試問題)
オヌシなら、まず何をする? 健闘を祈る!
攻略キーポイント
「幾何学に王道なし」とは古代ギリシャの哲学者ユークリッドの言葉じゃ。幾何学とは、算数・数学の図形分野のこと。ユークリッドは、当時の王様に幾何学を教えていたときに、王様が「簡単に幾何学を学ぶ方法はないのか」と質問され、こう答えたのじゃ。つまり、図形問題を解けるようになるには、どんなに偉い人でもコツコツ努力するしかないということなのでござる。その努力というのは、基本的な図形の性質を覚えて、たくさんの問題を解くことじゃ。これはサッカーに例えれば、パスやシュートの練習して、たくさんの試合でプレーすることに似ているのう。
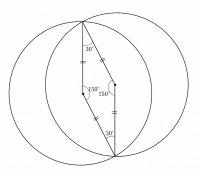
では今回の問題のキーポイントじゃ。1つの円では、半径がみんな同じ長さだということが、円の性質で1番大切なことじゃ。でも問題には半径が書いていないので、自分で半径を書き込んでみると良いぞ。問題を解決するために新しく書き加える線のことを「補助線」と呼ぶ。4本の補助線は半径なので 、半径に囲まれた四角形は、ひし形じゃ。
また、円を30°回転させているので、ひし形の4つの角度がすべてわかる。中心角が150°の2つのおうぎ形ひし形の部分で重なっていることが見えたら、あとはひし形の面積を求めるだけじゃ。
そのヒントは「補助線」。
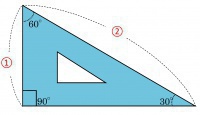
正三角形を半分にした三角定規では、1番長い辺は1番短い辺の2倍の長さになっている事ことを利用して、もう1本の「補助線」を書く。これは自分で探して見るのじゃ。
たった1本の「補助線」が、図形の性質を鮮やかに浮き立たせ、あっという間に問題が解決してしまうことがある。それが理解できた瞬間の感動は、オヌシを算数・数学のトリコにしてしまうはずじゃ!算数の問題は、自力で考え抜くからこそ、解けたときは本当に嬉しい。まずは「補助線」を書くことから始めるのじゃぞ!